Note

This tutorial is produced by the Jupyter notebook here.

What’s fit.py doing? The fitting procedure in detail

To give further insight into the fitting process in Frankenstein (frank) and how you can modify it, here we’ll use the code as a module and perform the same fit that’s in the Quickstart, just in more detail.

So we’ll keep using the DSHARP continuum observations of AS 209 (Andrews et al. 2018) as the input dataset, and frank will reconstruct the disc’s 1D radial brightness profile by nonparametrically fitting the real component of the visibility distribution.

Specifically frank will perform 4 steps in the fit, which we’ll break into distinct calls here (these are the steps taken in fit.py):

1. Parse the .json parameter file and read in the data (UVTable);

2. Determine the disc geometry (inclination, position angle and phase offset), then deproject the visibilities;

3. Fit the deprojected visibilities with a Gaussian process (it’ll take ~50 sec for this dataset) to yield a brightness profile;

4. Save the fit results and diagnostic figures. We’ll also supply a CLEAN brightness profile for the disc as well as the synthesized CLEAN beam parameters, in order to compare the frank fit to the CLEAN fit by:

   • Convolving the fitted frank brightness profile with the synthesized beam to compare to the CLEAN profile and

   • Taking the discrete Hankel transform of the CLEAN profile to compare to the frank visibility domain fit.

Let’s walk through these.

1. Read in the parameter values and data

As in the second example in the Quickstart - where we use frank as a module - we’ll import the internal classes FrankFitter and FitGeometryGaussian directly, in order to demonstrate their usage. Just note that fit.py uses the wrapper functions deproject_disc and perform_fit to call these, and more generally uses wrapper functions to do everything that we’ll walk through more verbosely here.

%matplotlib inline

import numpy as np

import frank
from frank.geometry import FitGeometryGaussian, FixedGeometry
from frank.radial_fitters import FrankFitter
from frank.fit import load_default_parameters
from frank.utilities import convolve_profile
from frank.make_figs import make_deprojection_fig, make_clean_comparison_fig

frank.enable_logging()

Using a UVTable extracted from an MSTable (see this tutorial for how to do this) and the default parameter file default_parameters.json, let’s read both in.

model = load_default_parameters()

as209_dat = np.load('AS209_continuum.npz')
u, v, vis, weights = [as209_dat[k] for k in ['u', 'v', 'V', 'weights']]

2. Determinine the disc geometry and deproject the visibilities

Before fitting the radial brightness profile, we need to determine the disc’s geometry (inclination, position angle and phase center) in order to deproject the visibilities (recall that frank, fitting in 1D, assumes an axisymmetric source). To do this we pass an object specifying how the geometry is determined to the FrankFitter class. The position angle (PA) is defined positive east of north, and the right ascension offset (dRA) is defined positive for offsets toward east.

frank has three classes for this: FixedGeometry just takes a geometry you provide, FitGeometryGaussian determines the geometry by fitting a 2D Gaussian directly to the visibilities, and FitGeometryFourierBessel determines the geometry by fitting a nonparametric form.

FitGeometryFourierBessel is a more robust approach than FitGeometryGaussian, as the former fits for the geometry without making any assumptions about the functional form of the visibilities. Note that as ``FitGeometryGaussian`` fits a 2D Gaussian to the visibilities to determine the geometry, it is not a good choice for a highly non-Gaussian disc (like a disc with an inner cavity). There is a tradeoff in speed for using FitGeometryFourierBessel; even for large datasets (of order \(10^7\) visibilities), FitGeometryGaussian takes only \(\approx 30\) sec, while FitGeometryFourierBessel takes \(> 10\) min. It’s also useful to determine the geometry in the image plane and compare to the result from frank. You can also supply your own geometry fitting routine (see Sec.2.1 below).

For FitGeometryGaussian and FitGeometryFourierBessel you can choose to provide a known phase center if you just want to fit for the inclination and PA (if running frank from the terminal, set geometry : fit_phase_offset to false in your parameter file and specify dra and ddec there). You can conversely supply the phase center and just fit for inclination and PA.

You can also supply an initial guess for the source geometry; if running frank from the terminal, setting geometry : initial_guess to true in your parameter file will use the inc, pa, and optionally dra and ddec in that file as the initial guess for the geometry solver. Below we’lls assume we don’t know or have a guess on any of the disc’s geometry parameters, and so fit for them all.

Note that, by default, the visibility deprojection in frank scales the total flux assuming that the disk is optically thick everywhere. Since an inclined optically thick disk covers less area on the sky, the total brightness should be lower by a factor \(\cos(i)\). We can see this by considering the solution to the radiative transfer equation for a razor-thin disk (as is assumed in frank), \(I(r) = e^{-\tau(r)\ /\ \cos(i)}\). For a face-on disk, \(i = 0\) and the brightness at all radii scales inversely with the optical depth \(\tau\), as expected. Conversely, in the limit that the disk becomes edge-on (\(i \rightarrow 90^\circ\)), the brightness tends toward \(0\).

Internally in frank, this correction is done by scaling the observed visibility amplitudes by a factor \(1 / \cos(i)\) and their weights by \(\cos(i)^2\). When using frank to compute the visibilites for the model (the ‘predicted visibilities’), this scaling will automatically be applied to the model visibilties so that their amplitude matches the observed visibilities. This option is the default because it produces an intensity profile that is consistent with one extracted directly from a 2D image (such as an azimuthal average or major- or minor- axis cut). If you instead wish to not rescale the visibilities, as appropriate for an optically thin disk, set geometry : rescale_flux to false in your parameter file.

geom = FitGeometryGaussian()
geom.fit(u, v, vis, weights)

print('Fitted geometry: inc  = {:.2f} deg,\n\t\t PA   = {:.2f} deg,\n\t\t'
      ' dRA  = {:.2e} mas,\n\t\t dDec = {:.2e} mas'.format(geom.inc, geom.PA,
                                                           geom.dRA*1e3,
                                                           geom.dDec*1e3))

    Fitting Gaussian to determine geometry

Fitted geometry: inc  = 33.93 deg,
                 PA   = 86.47 deg,
                 dRA  = -8.63e-01 mas,
                 dDec = 2.29e-01 mas

The published values (Huang et al. 2018) are a bit different:

      inc = 34.97 deg,

      PA = 85.76 deg,

      dRA = 1.90 mas,

      dDec = 2.50 mas

So let’s use those.

geom = FixedGeometry(34.97, 85.76, 1.9e-3, 2.5e-3)

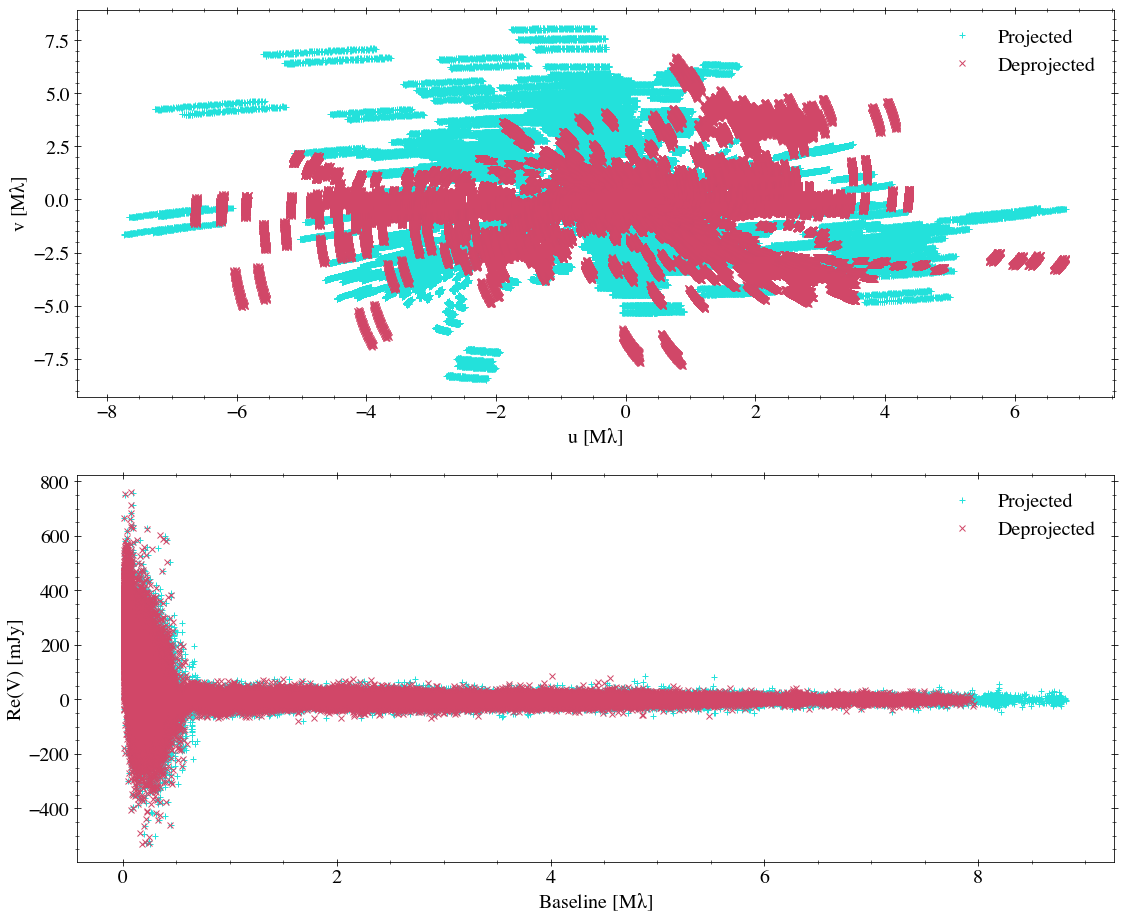
Using the published geometry, we’ll plot the deprojected (u, v) coordinates and visibilities - unbinned - just to see roughly how much the correction is affecting the (u,v) coordinates and visibility amplitudes. Note that FrankFitter (which we’ll use below) deprojects the visibilities as a step in the fit; this figure will just redundantly deproject them (using geom.apply_correction) to make the plot.

If running frank from the terminal, you can produce this figure by setting deprojec_plot to true in your parameter file.

make_deprojection_fig(u, v, vis, weights, geom, bin_widths=[], figsize=(16,14), force_style=False);

    Making deprojection figure

2.1 Adding your own geometry fit routine

You can extend frank’s geometry fitting capabilities with your own routines by writing a class that inherits from the SourceGeometry base class. This base class provides the interface used by frank to deproject the visibilities, but you do need to implement your own fit() method. This method will be called internally by FrankFitter to determine the geometry.

The fit() method should set the attributes _inc, _PA, _dRA, and _dDec – in respective units of [deg], [deg], [arcsec], [arcsec] – that are used by the apply_correction(), undo_correction(), deproject(), and reproject() methods.

3. Fit the deprojected visibilities for the brightness profile

Now that we have the deprojected visibilities, let’s fit them.

Objects used to perform a fit are in the FrankFitter class. In addition to the the geom object detailed in Sec.2, five hyperparameters affect the fit: Rmax and N, which set the disc radius out to which the fit is performed and the number of collocation points used in the fit; and alpha, p_0 and weights_smooth, the hyperprior parameters on the power spectrum prior. See the frank methods paper for an explanation and interpretation of these five hyperparameters, and this tutorial for a demonstration of how to test their effect on a given fit.

frank performs a fit with the FrankFitter class’ fit() function. Let’s use this with the geom object we generated above using the published geometry values, Rmax = 1.6" appropriate for AS 209, N = 250 to ensure we resolve narrow features in the brightness profile, and the default values p_0 = 1e-15 Jy\(^2\), alpha = 1.05 and weights_smooth = 1e-4. Recall that we’ll only fit the real component of the visibilities, as frank is assuming an axisymmetric source that has zero imaginary component.

Rmax, N, alpha, weights_smooth = 1.6, 250, 1.05, 1e-4

# Initialze the FrankFitter class
FF = FrankFitter(Rmax, N, geometry=geom, alpha=alpha, weights_smooth=weights_smooth)

# Fit the data, returning the maximum a posteriori solution object
sol = FF.fit(u, v, vis, weights)

  Fitting for brightness profile using FrankFitter
    Building visibility matrices M and j

    FrankFitter iteration 692

    Convergence criterion met at iteration 692

Once the fit is complete, the brightness profile’s best fit parameters are returned and stored in the FrankFitter class’ MAP_solution object (we called it sol above). This provides:

• the maximum a posteriori solution and posterior covariance for the reconstructed brightness profile;

• the fit’s radius points r and corresponding frequency points q;

• methods to compute the best fit model’s visibilities at given (u, v) coordinates in either the sky plane with predict or the deprojected plane with predict_deprojected;

• and a method to evaluate the best fit model’s log_likelihood.

Additionally the FrankFitter object we created (we called it FF) contains the power spectrum’s best fit parameters:

• the maximum a posteriori power spectrum mean (MAP_spectrum) and covariance (MAP_spectrum_covariance).

4. Save the results and generate plots

We could now save the fit results, including the sol object, with save_fit(u, v, vis, weights, sol, prefix='AS209_continuum'). We could also produce a full diagnostic figure and/or simplified figure of the fit. But since we’ve already done all this in the Quickstart, let’s instead use the sol object to make a figure comparing the frank fitted brightness profile to the published CLEAN image-extracted profile (Huang et al. 2018).

If running frank from the terminal, you can produce this figure by setting, in your parameter file, compare_profile to the path to a file with a CLEAN profile (or any comparison profile) and clean_beam to the beam parameters (FWHM along both axes, position angle).

# Load the CLEAN radial profile for AS 209
r_clean, I_clean = np.genfromtxt('./AS209_clean_profile.txt').T
clean_profile = {'r':r_clean, 'I':I_clean, 'lo_err':None, 'hi_err':None}

# Using the same disc geometry parameters as above (the published values)
# and the CLEAN beam parameters from CASA (`imhead` of the published .fits file),
# convolve the frank profile with the CLEAN beam
# Units: [arcsec], [arcsec], [deg]
clean_beam = {'bmaj':0.03883, 'bmin':0.03818, 'beam_pa':85.82243}
mean_convolved = convolve_profile(sol.r, sol.mean, geom.inc, geom.PA, clean_beam)

# For the visibility plot, show the observations in 1 and 50 k\lambda bins
bin_widths = [1e3, 5e4]

# And for the 2D representations of the 1D profiles, use a colormap with an arcsinh
# normalization, including a choice of the arcsinh scale parameter, 'asinh_a'
stretch = 'asinh'
asinh_a = 0.02

# Distance to source [pc] (Andrews et al. 2018), just to show a second x-axis in AU
dist = 121.

# Zoom in on the lower amplitude visibilities to better see the fit accuracies at long baselines
ylims = [-20, 20]

make_clean_comparison_fig(u, v, vis, weights, sol, clean_profile,
                          bin_widths=bin_widths, stretch=stretch, mean_convolved=mean_convolved,
                          dist=dist, ylims=ylims, force_style=False, figsize=(16,16));

    Making CLEAN comparison figure

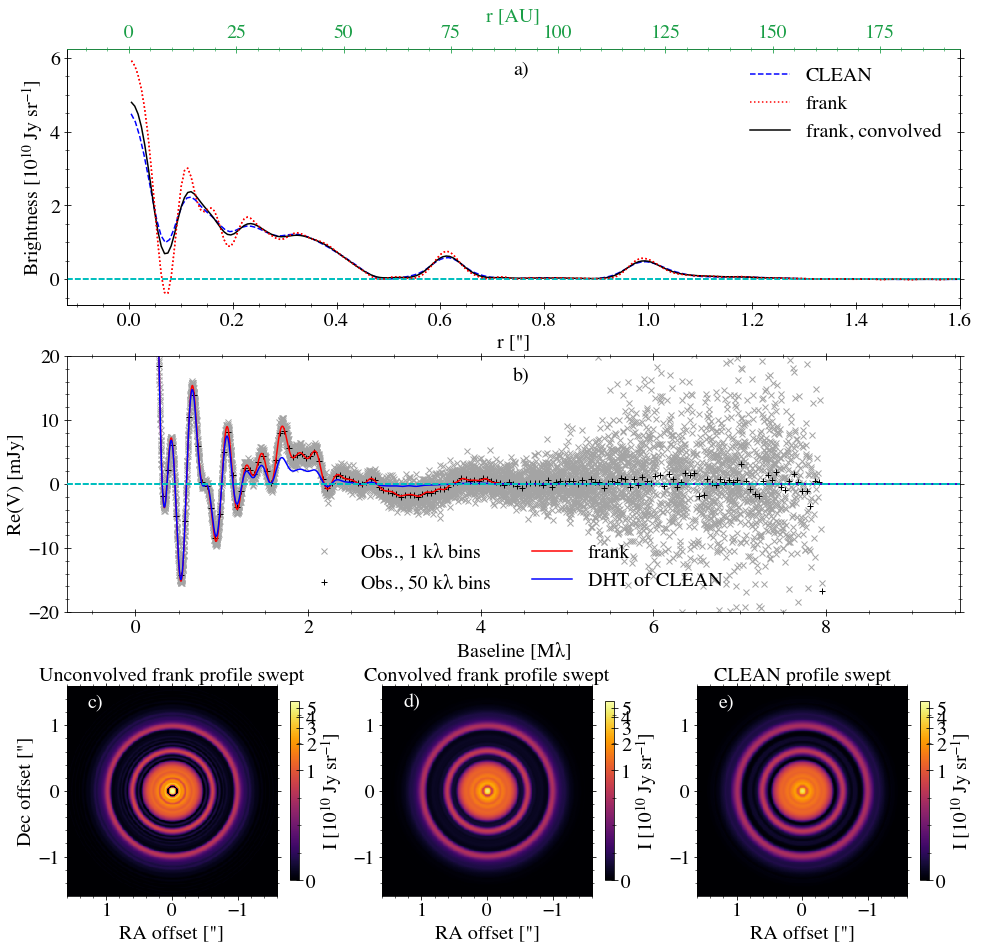
a) The frank profile, this profile convolved with the CLEAN beam, and the CLEAN profile. The frank profile when convolved with the CLEAN beam is pretty similar to the CLEAN profile, an indication that the unconvolved frank profile is correctly identifying sub-beam structure. The observartions are shown in \(1\) and \(50\) k\(\lambda\) bins.

b) The binned, observed visibilities, the frank visibility domain fit, and the discrete Hankel transform (DHT) of the CLEAN profile. Relative to the frank fit, the DHT of the CLEAN profile is low beyond \(\approx 1\times 10^6 \lambda\), primarily because of beam convolution. This is another indication that the frank brightness profile is accurately recovering sub-beam structure.

c) The unconvolved frank profile swept over \(2 \pi\) to generate a face-on, 2D representation of the 1D profile. Note this is not an image generated by CLEANing the frank fitted visibilities. The colorscale is the same across (c) - (e) for comparison.

d) The frank profile convolved with the CLEAN beam, then swept over \(2 \pi\). As expected, the 2D sweep has annular features that are less sharply defined that in (c) because convolving the frank profile effectively degrades its resolution.

e) The CLEAN profile swept over \(2 \pi\). This is not the CLEANed observation, just a 2D representation of the CLEAN profile for comparison with (c) - (d).